
According to Serge Stauffer’s Duchamp: Gesammelte Schriften, the originals of these pages are currently at The Foundation for Contemporary Performance Arts, New York.
My reasons for interpreting each Roman numeral I-VIII as a single line are that:
- He is trying to create “une sorte d’alphabet musical nouveaux”. Alphabets are single sequences of letters — not polyphonic.
- His comment that “l’ordere de succession est (au gré) interchangeable” makes
sense in that, when the “period” consists of 2 or 3 “periodes fragmentées”,
the order in which the numbers are taken from the sub-selections can be varied: for example, III
has three “periodes fragmentées”:

which can be ordered
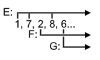
or
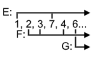
etc.
In the realisations below, I generally distribute each sub-selection evenly along the finished line. This makes for a relatively even curvature along the line, but is not essential.
I’m assuming that Duchamp is using the word period in the musical sense (as in “an 8-bar period”). In other words as an abstract, limited sequence unrelated to absolute units of time (hours, minutes, seconds). In music, such periods can vary considerably in duration, depending on how they are performed. - A close parallel to the idea of the 3 Stoppages-étalon becomes evident.
Note that Duchamp started (in I) by writing two clefs on manuscript paper, and then decided to use numbers instead. The Erratum musical for Yvonne-Magdaleine-Marcel predates these pages, so it looks as if he originally intended to use musical notation as in the earlier work, but decided against that because numbers are easier to notate and manage.
I think its unlikely that he used these numbers for anything - otherwise there would be some signs on the score indicating which of the notes he had used (crossings out etc.).
The instructions at the end of page 2 (see The Apparatus below) are written in three clearly separate paragraphs which were probably written after he had completed VIII (otherwise the spacing on the page would have been different). The first paragraph is a simple explanation of what the numbers represent. The second paragraph is the beginning of an attempt to be more precise about how these numbers could be used to realize a peformance (he’s thinking aloud).
I think the third text, with the sketch for an apparatus, may have been added much later (days or weeks) — he may have added the title on page 1 at the same time (similar handwriting).
The “appareil enregistrant automatiquement les periodes musicales fragmentées” seems to me to be an attempt to embody the principles he’d been developing in I-VIII in an object — as a visual artist he wanted things, not just concepts. Interestingly its an object that is intended to be operated in time.
Strangely, the idea of ordering the contents of each wagon before its use, is not mentioned in connection with the appareil (perhaps, by then it was too obvious), and there are more wagons than are used in any of the selections I-VIII. Perhaps he was thinking of investigating the matter further — with more wagons and a finer-grained selection of pitches (1/4 tones).
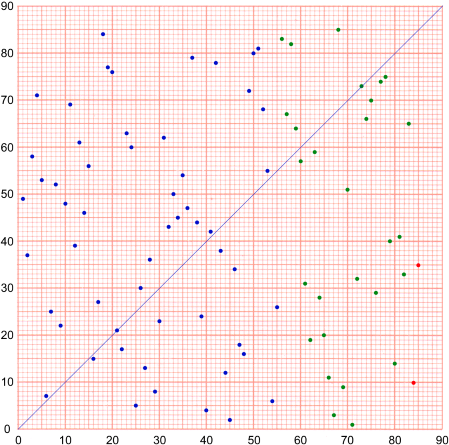
 Here, B contains the values 10 and 35 together with 28 other numbers selected randomly from the 85.
Selection A contains the remaining 35 numbers in random order.
Here, B contains the values 10 and 35 together with 28 other numbers selected randomly from the 85.
Selection A contains the remaining 35 numbers in random order.Selection A is followed by B. I followed his instructions, putting the values 10 and 35 at the end of B.
This strategy introduces the idea of partitioning the total selection, but is as yet no better than simply selecting all the values in random order.
These numbers are in the left-right order of my 1979 scale I.
Selection II
 Here, the first 25 numbers were selected at random for D, then the remaining 60 were selected in
random order for C. Note that both the C and D numbers are evenly spaced, indicating that they were
written in the order they were selected. He left himself plenty of space for the 60 C-numbers. The
fat “barline” at the end of C indicates that it is a single sub-sequence, not two separate
sequences.
Here, the first 25 numbers were selected at random for D, then the remaining 60 were selected in
random order for C. Note that both the C and D numbers are evenly spaced, indicating that they were
written in the order they were selected. He left himself plenty of space for the 60 C-numbers. The
fat “barline” at the end of C indicates that it is a single sub-sequence, not two separate
sequences.Duchamp may have originally intended C to be followed by D (as in I A and B), but have noticed that since their components are in random order, C and D could just as well be simultaneous.
Note that the curly bracket at the start of the system is a correction.
These numbers are in the left-right order of my 1979 scale II.
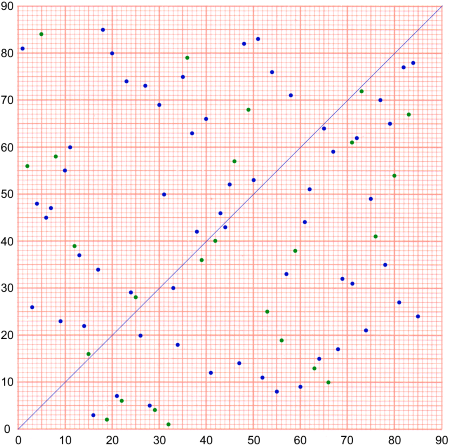
 This is where things begin to get interesting! Here, there are three sub-selections, with G
containing just 6 and 60. (G’s order may or may not have been deliberately ascending).
This is where things begin to get interesting! Here, there are three sub-selections, with G
containing just 6 and 60. (G’s order may or may not have been deliberately ascending).F contains the next fourteen numbers deliberately arranged in ascending order. This can be seen from their spatial arrangement. He wrote the numbers as they were chosen, at positions that would allow him to put the following numbers in order. The spacing has nothing to do with either vertical alignments or absolute time.
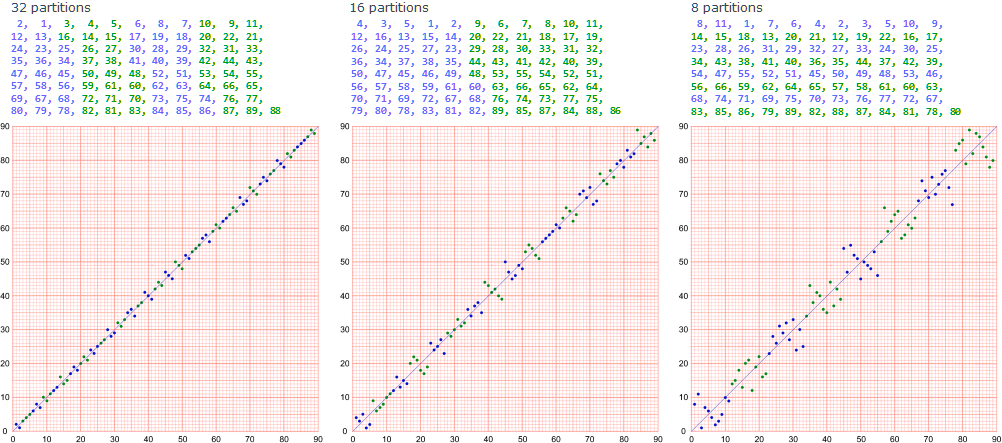
The idea of creating randomly ascending “periodes fragmentées” is further improved in E. Here he made nine partitions (the beginning of the idea for wagons) arranged in ascending order and then filled them randomly. The first partition contains the numbers 1 to 9, the second the numbers 10-19 and so on, the last partition containing 80-85.
It is possible that the idea for partitions came as a result of his experience with F, since they arise when numbers are written on paper in positions that are estimated in relation to their value. Note that E effectively consists of a non-random sequence of random sequences — like A followed by B in Sequence I, except that each subsequence is in a range higher than its predecessor. This gives a marked direction to the sub-sequence (E) as a whole, without individual notes in the sub-sequence being necessarily higher than their predecessors (as in F). E and F certainly show the direction in which his thoughts are moving. Even if he was not thinking in terms of the Stoppages-étalon at the beginning, by now he is!
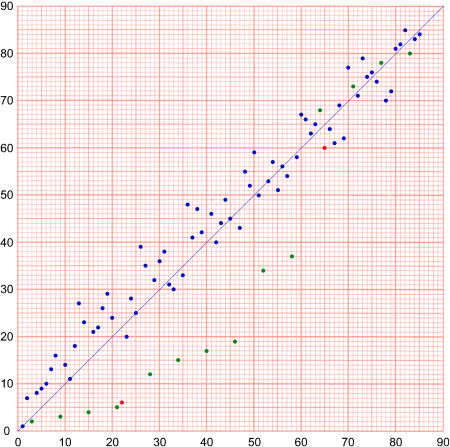
 He reverts to two sub-selections (G is rather ineffectual in III), but the general principle remains
the same. He seems, within the partitions in H to have tried to compromise between randomness and
straightness: The partition for 10-19 is completely straight (ascending), and has the typical
spacing for a straight selection — note that he put the 10 at the end of the 1-9 partition.
Partitions 1-9, 50-59 and 60-69 are straight except for one value (in 1-9 its the first value, in
50-59 and 60-69 its the last value).
He reverts to two sub-selections (G is rather ineffectual in III), but the general principle remains
the same. He seems, within the partitions in H to have tried to compromise between randomness and
straightness: The partition for 10-19 is completely straight (ascending), and has the typical
spacing for a straight selection — note that he put the 10 at the end of the 1-9 partition.
Partitions 1-9, 50-59 and 60-69 are straight except for one value (in 1-9 its the first value, in
50-59 and 60-69 its the last value).Partitions 20-29 and 50-59 are straight except for two values (in 20-29 the first and last values, in 50-59 the eighth and last values).
Partitions 70-79 and 80-85 have been amalgamated (note that the divider has been crossed out).
Possibly, he was trying out the use of smaller ascending partitions:
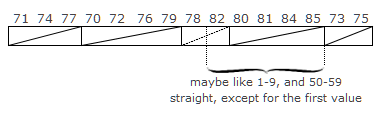
He may have mentally divided the 70s block into two straight segments plus one value... or possibly these are simply random values within the 70s. In any case, the straightness within most of the partitions is very marked, and I think it is indisputable that in IV he was somehow using the straightness (first used in III F) one level lower (at the level of the partitions).
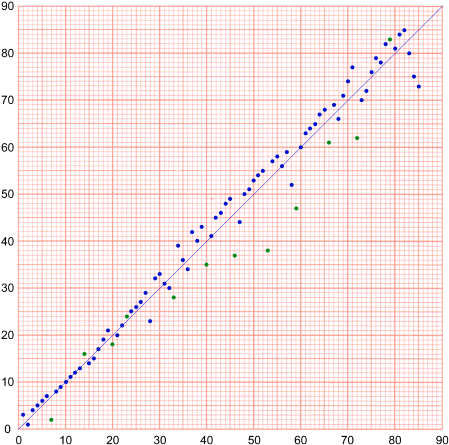
 If all the partitions in IV had been completely straight, sub-selection H would have been a
single chromatic scale from 1-85 except for the values in sub-selection I. This is what I think
happens now.
If all the partitions in IV had been completely straight, sub-selection H would have been a
single chromatic scale from 1-85 except for the values in sub-selection I. This is what I think
happens now.I think both J and K are in ascending order, and that J did not have to be written out because it is nearly a chromatic scale.
Selection V is crooked because the values in K have effectively been moved from their standard positions. Here, he effectively starts with a straight line, and then proceeds to bend it. (Did the Stoppages-étalon come after this Erratum musical?) Notice that although K is ascending, it has not got the typical spacing for a straight sequence. He may have just kept and sorted the number tokens before writing out their values, or written their values on a separate piece of paper. He may have already started using a separate page for intermediary results in order to cope with the complexities of sub-selection IV H (note the spacing there).
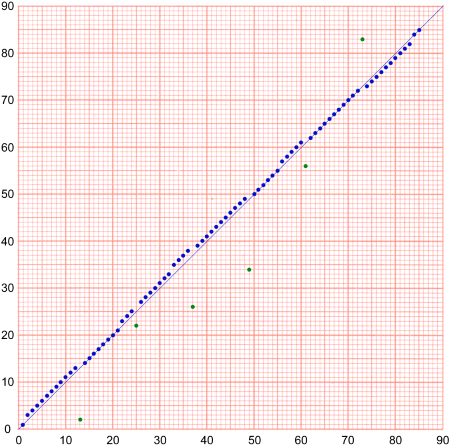
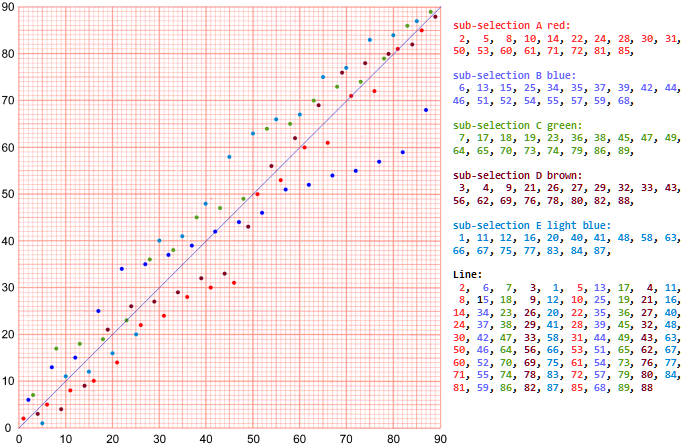
Note that as with all the other selections except III, the three selections VI, VII and VIII each consist of two sub-selections (périodes fragmentaires). The sketch for The Apparatus prescribes 5 or 6.
I think the first two texts below VIII refer to Selections I-VIII, and that The Apparatus is a later, incomplete addition (à developer) that should be treated separately. Note the different handwriting.
 Sub-selection L contains the first 11 randomly chosen numbers in numerical order.
Sub-selection L contains the first 11 randomly chosen numbers in numerical order.M contains the remaining 74 numbers (from 85) in numerical order.
Duchamp seems to have changed his mind here. A number between 8 and 20 has been deleted, so that L only contains 11 numbers, not 12.
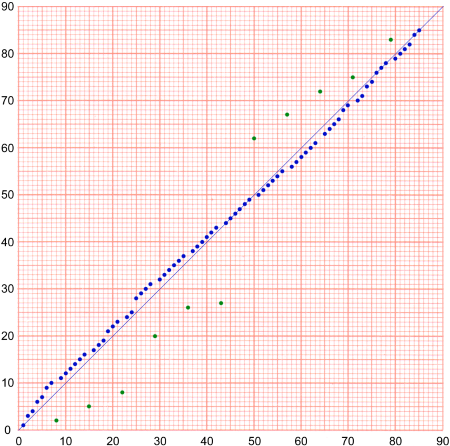

Sub-selection O contains the first 22 randomly chosen numbers in numerical order.
N contains the remaining 63 numbers in numerical order.
The number 65, to the left of the O staff, could be the number of numbers in a (randomly selected) pre-selection, from which he selected the first 22.
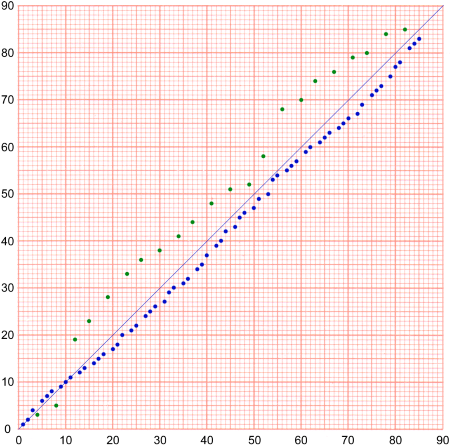

Sub-selection Q contains the first 10 randomly chosen numbers in numerical order.
P contains the remaining 75 numbers in numerical order.
The number 40, to the left of the Q staff, could be the number of numbers in a (randomly selected) pre-selection, from which he selected the first 10.
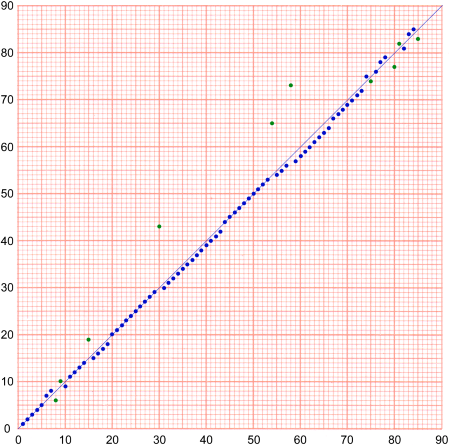

Each n° indicates a note; an ordinary piano contains about 89 notes; each n° is the number in
order starting from the left.

Unfinishable; for a designated musical instrument (player piano, mechanical organs or other new
instruments for which the virtuoso intermediary is suppressed); the order of succession is (to
taste) interchangeable; the time which separates each Roman numeral will probably be constant (?)
but it may vary from one performance to another; a very useless performance in any case.

An apparatus automatically recording fragmented musical periods
Vase containing the 89 notes (or more: 1/4 tone) figures among n° on each ball.
Opening A letting the balls drop into a series of little wagons B.C.D.E.F. etc
Wagons B, C, D, E, F, going at a variable speed, each one receiving one or several balls
When the vase is empty: the period in 89 notes (so many) is inscribed and can be performed by a designated
instrument
another vase - another period - the result from the equivalence of the periods and their comparison a kind of new musical alphabet allowing model descriptions. (to be developed).
I think Stauffer is probably right but that the difference does not affect the following argument.
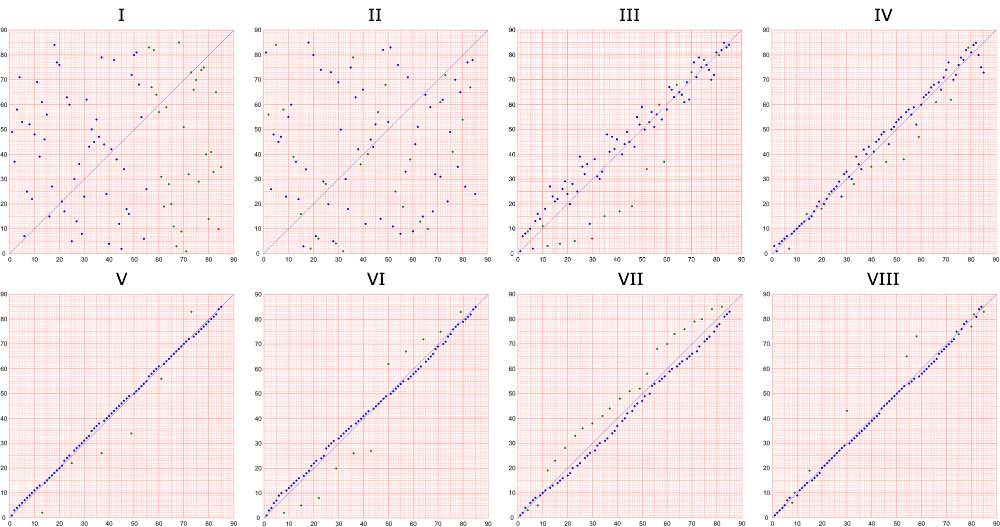
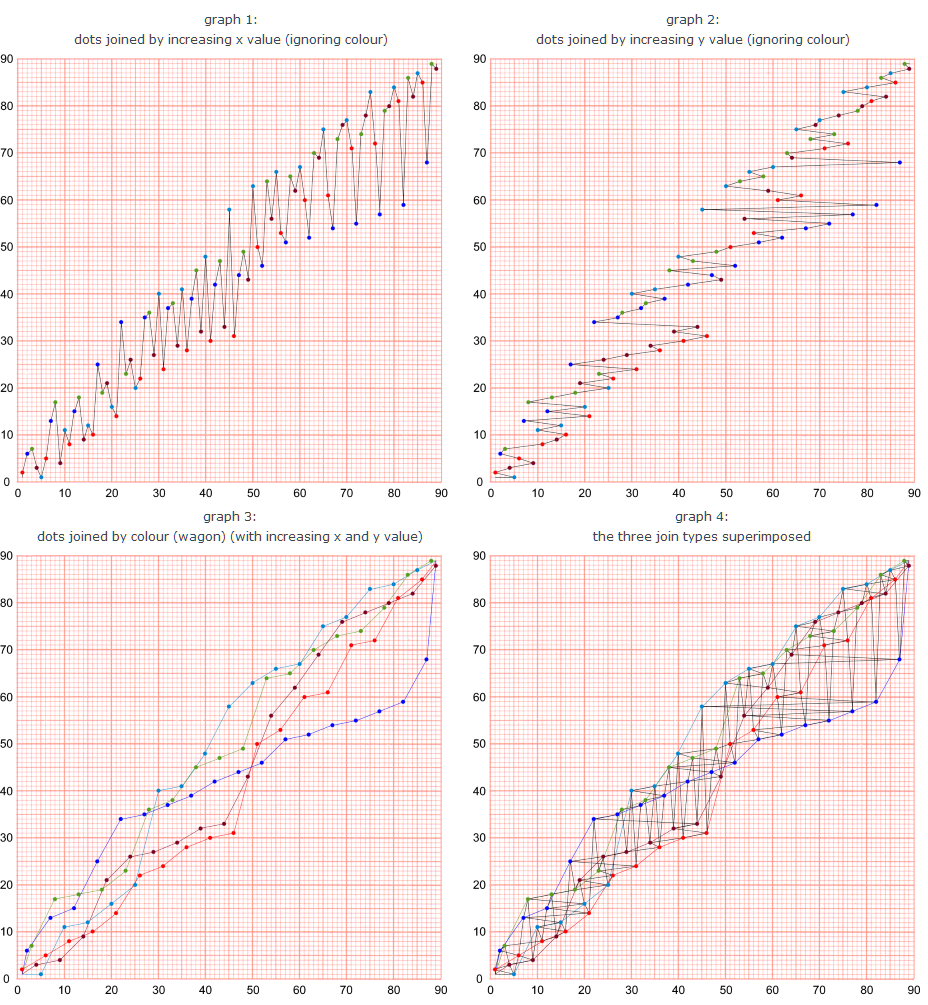
Notice that the content of each wagon (whose values are random as to number and the order in which they are observed) can be used to define an erratic path between points (1,1) and (89,89).
Until they are known, all that can be said about the values is that they exist in a probabilistic field.
The characteristics of this field can be changed by
- Ignoring the time at which the wagons are evaluated (by plotting each wagon’s content on the same graph). Note that another vase is another period, so a period is defined by all the wagons.
- Ignoring the time at which the values inside the wagons are evaluated (by always putting them in ascending order — as in sub-selections L, M, N, O, P, Q)
- The number of values in each wagon is as equal as possible.
- Each wagon’s values are ordered numerically and distributed as equally as possible horizontally.
Note that:
- Indicating that two dots are in sequence does not have to be done with a straight line. There is, in fact, no single “correct” way to do this! (see below)
- The paths joining (1,1) to (89,89) in graph 3 are much shorter than the black paths in graphs 1 and 2.
- The direct diagonal between (1,1) and (89,89) can be created by collapsing graph 1 (horizontally) and graph 2 (vertically). Any of the coloured paths can be collapsed either horizontally or vertically onto the same direct diagonal, but using fewer dots.
- There are other ways to define dot sequences (absolute proximity, various diagonals etc.) but they all involve ambiguity unless the colour is taken into account: Situations will always arise in which there can be more than one dot that fulfils the “next dot in sequence” requirement.
I agree very much with Hoffman, that our perceptions are probably an interface that shields us from ultimate, physical reality: we throw away all the information we can’t cope with and then mentally join the dots. Space and time are a brain strategy for reducing complexity.
Note that:
-
Even though random numbers can be used while modelling otherwise inscrutable information,
that does not mean that we have understood the inscrutable information! We all agree on and use the results of scientific
experiments (quantum physics is highly successful), so its probably not “random” in the same way!
Gott würfelt nicht!
[added 31.01.2019]: See also Duchamp’s comments on chance, as reported in Serge Stauffer’s Duchamp: Gesammelte Schriften (page 97, footnote 92): ”Ihr Zufall ist nicht der gleiche wie mein Zufall, genau so wie Ihr Wurfelwurf selten der gleiche sein wird wie der meine.“ Stauffer says that the original is in "Tomkins 1965, seite 58" — which I have been unable to find. My back-translation would be: “Your chance is not the same as my chance, in the same way as your throw of the dice will seldom be the same as mine.” — if anyone knows where the original quote can be found, please let me know.
Stauffer’s Anmerkungen to this footnote lead eventually to Poincaré and Jouffret... - When listening to music or speech, we automatically chunk the incoming information (a continuous sound wave) so as to create points (symbols) that we then connect to each other to create higher levels of meaning. We seem to need the flexibility to ignore or create some of these levels. Chunking and joining the dots are opposite strategies.
Bent lines, that can be usd in the same way, can be created simply by interpolating values between the values in a single sub-selection (the sub-selection in a single wagon). This can be done by drawing either straight or curved lines between the values. However, straight lines are not the best solution if we are looking for minimum energy paths, because the line segments that meet at a knot have no common tangent, so an energy impulse would be required there to change the direction.
A curve that is often used in engineering is the cubic spline — as in the following diagrams.
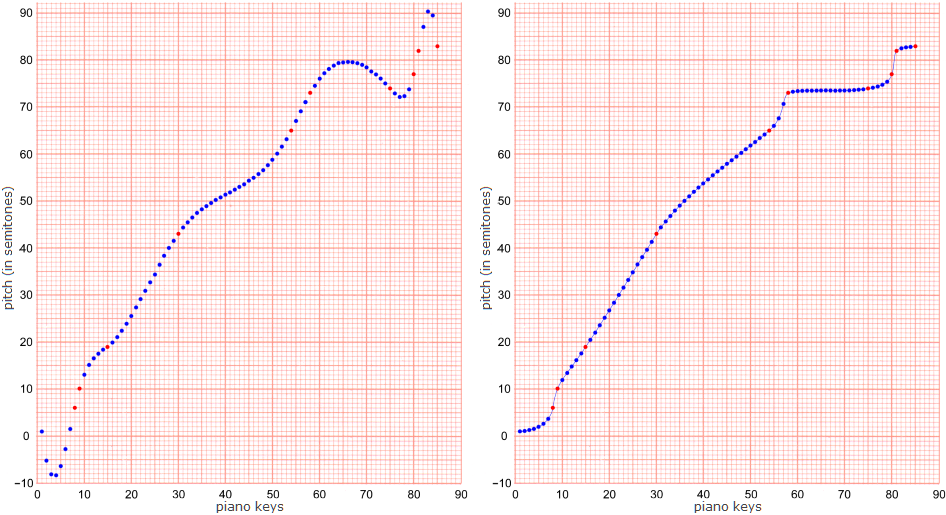
Duchamp's Selections VI, VII and VIII were, I think, intended as “standard stoppages”, so I have used the points from sub-selections VI (L), VII (O) and VIII (Q) (coloured red) in the following diagrams. Note that, in contrast to Duchamp's procedures, this results in microtonal pitches on the y-axis. It would, of course, be possible to round the values to the nearest semitone or quarter-tone etc...
The diagrams on the left were constructed using data from a cubic spline interpolation utility.
Those on the right were drawn freely such that the slope is always positive, using the cubic spline tool in Paint.net (version 4.1.5) — see Splines below.
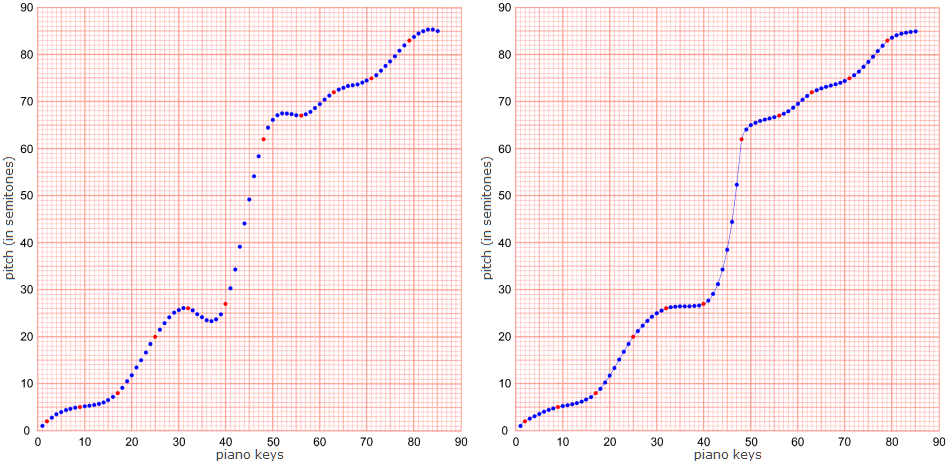
Interpolating one pitch per piano key between the values of sub-selection O in Erratum musical VII:
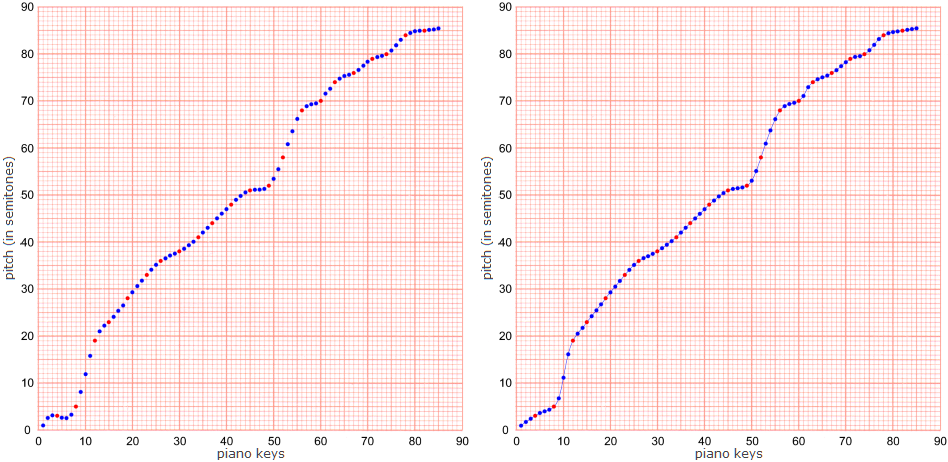
Interpolating one pitch per piano key between the values of sub-selection Q in Erratum musical VIII:
All the possible paths through a particular series of knots have the same fixed points at the knots, but they are increasingly different in-between. It is possible to think of this blurring between the knots as a kind of wave of uncertainty that collapses when a particular curve is chosen. The act of choice fixes a moment in time. A Stoppage is thus the record of a moment. It "collapses the wave function" that is all the possible configurations of Duchamp's string as it falls to the ground.
If the method chosen to create the “kind of new musical alphabet allowing model descriptions” is to select just one of the wagons from the stopped Erratum Musical Apparatus, then we have to think of the Apparatus as containing a probability field even when it has stopped.






.png)


